【STL源码剖析】系列八:序列式容器--heap和priority_queue
前言
本篇首先介绍STL中优先级队列(priority queue)的底层实现组件——heap,主要内容有:
1.堆的概念以及实现方式(一个容器vector和一组操作算法),STL中实现的是大顶堆;
2.堆的操作方式:push_heap、pop_heap、sort_heap以及make_heap;
3.补充介绍堆排序算法,时间复杂度为O(logn)。
接着介绍STL中的priority_queue(优先级队列),由于是在底层容器的基础上加上heap方法,因此优先级队列是一种适配器。
heap
heap概述
heap并不是一种STL容器,引入它的目的是为了实现priority queue(优先级队列)。
优先级队列允许用户以任何次序将元素装进容器内部,但是取出时一定是将优先级最高的元素先取出。而大顶堆恰好具有这样的性质,因此STL中实现的是大顶堆。
堆的定义是:一颗具有如下性质的完全二叉树:每个节点的值都大于或等于其左右孩子的值,称为大顶堆;每个节点的值都小于或等于其左右孩子的值,称为小顶堆。
完全二叉树具有这样的性质:假设一共有n个元素,下标从1~n,那么对于一个节点 i 来说(i 大于等于1,小于等于n / 2),其左孩子的下标为2i,右孩子的下标为2i + 1,其父节点的下标为i/2。因此可以使用vector来保存完全二叉树的n个节点。(使用vector是因为array不具有动态改变大小的功能,而一个堆增加元素时可能需要动态增长空间。)
综上,实现一个堆需要一个vector作为底层容器,以及一组heap算法来调整其中的元素顺序。
heap算法
push_heap算法
当向堆中插入一个元素时,首先将这个元素插入到最后一层的从左到右的第一个空位置上,也就是底层容器vector的end()处。
插入之后,需要调整这个新元素的位置,让其满足大顶堆的定义。因此执行一个上溯的过程:将新节点与父节点比较,如果值比父节点大,就父子对换位置;这样一直上溯,直到不需要对换或者直到根节点为止。
下面是push_heap算法细节,接受两个迭代器,分别表示底层容器vector的头和尾,并且假设新元素已经在vector的尾:

关于上面计算父节点序号的解释:
这里first迭代器作为序号1,0号位置为空。这里 first + holdIndex为最后一个元素的位置。
此时有:(1)(first + holdIndex) / 2 = P;(2)(holdIndex - 1) / 2 = parent;(3)P = first + parent
因为first为1,因此可以得到(3)等式两边是相等的。
这样做的好处是:如果使用两个迭代器来进行运算,中间会涉及到很多次迭代器加减运算;如果使用两个下标进行运算,仍然需要通过迭代器找到相应的元素;所以这里采用的是一个迭代器(first)和一个下标(holdIndex)的方式。
pop_heap算法
当从堆中取出一个元素时,由于这里是大顶堆,因此一定是取关键值最大的元素,而这个元素一定在根部,也就是第一个元素。
将这个元素取出实际上是将其移动至底层容器的最后一个位置,而原来在这个位置上的元素(堆的最下一层的最右元素)需要重新找到一个合适的位置。这里执行一个下溯程序:将原本在底层容器的最后位置的元素(也就是堆的最下一层的最右元素)填充至根节点的位置,然后与两个孩子节点比较值,与较大的值对换;然后更新位置,重新比较,直到两个孩子的值均小于当前父节点。
下面是pop_heap算法细节,接受两个迭代器,分别指向底层容器vector的头和尾:




注:我不同意侯捷先生的说法。这是因为在while循环结束之后的这一段代码的缘故:首先,循环结束时,first+holdIndex指向的是需要被插入的结点位置,此时只可能有两种情况:
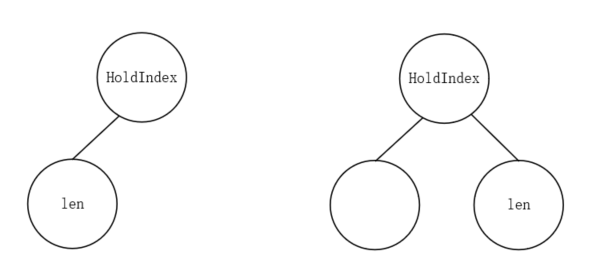
如果是上图左边的情况,循环结束的代码什么也不做,可以直接令value插入到holdindex的位置;
如果是上图右边的情况,循环结束时的代码就会使得holdIndex移动到左孩子的位置,令左孩子为根结点的值。注意,这里len的位置最开始时就是value的位置(此时是原来根节点也就是最大值的位置),value与其左兄弟之间的大小不可知,但是循环结束的代码强制令holdIndex的位置移动到左孩子的位置,因此需要调用push_heap函数,这个函数会尝试比较value和其根节点的大小,调整其位置。
总结,当pop_heap之后,最大的元素放在了底层容器的尾端,并没有被取走。如果想要取值,可以调用vector的back函数,如果想要移除,可以调用vector的pop_back函数。
sort_heap算法
从上面的pop_heap算法可以知道,每次取最大的元素放在最后的位置。如果持续对于整个堆进行pop_heap操作,每次操作范围从后向前缩减一个元素,那么当结束时,就可以得到一个递增序列。(这里其实就是堆排序的思想)
下面是sort_heap的算法细节,同样是接受两个迭代器,分别表示底层容器vector的头尾:

注意,sort_heap之后,此时已经不再是一个堆,而是一个递增序列。
make_heap算法
该算法就是将一段数据转换为一个堆。(也就是堆排序中对于待排序序列构造堆的过程)


heap没有迭代器
heap中的所有元素都遵循特定的排列规则,所以不允许遍历,因此不提供迭代器。
补充:堆排序算法
堆排序算法分为两部分:首先将数据转换为堆,然后一个循环不断调整元素顺序。

注1:假设有n个节点需要构成一个堆,那么根据二叉树的第5个性质,第n个节点的父亲节点一定是n / 2向下取整,也就是所有的父亲节点数目。
注2:构建堆时,从最后一个父亲节点开始构造,也就是从下向上、从右向左的顺序。

比如上面这张图,按照分别以30、90、10、50为节点进行构造堆,也就是第4、3、2、1个节点作为根节点构造堆。
将无序序列调整为堆:

时间复杂度分析:




prority_queue
概述
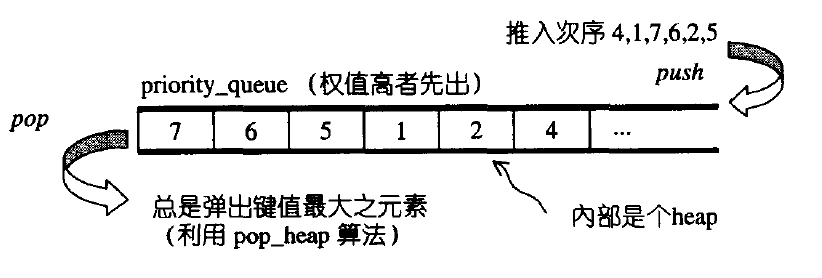
优先级队列带有权值概念,其中的元素不是按照推入的次序排列,而是按照元素的权值(通常权值以实值表示)排列,权值最高排在前面。
默认情况下优先级队列使用一个大顶堆完成,大顶堆的底层实现是由一个vector表现的完全二叉树。

priority_queue完整定义
优先级队列的实现由底层容器和heap算法处理完成,所以实现非常简单。默认情况下底层容器是vector。
(由于优先级队列也是在底层容器的基础上修改对外接口,因此优先级队列也是一种配接器)


priority_queue没有迭代器
由于优先级队列中的元素按照一定的规则排列,因此不允许遍历,也就不提供迭代器。