【STL源码剖析】系列十二：关联式容器--hashtable

发表于 2023-11-10 更新于 2024-04-20 分类于 STL源码剖析阅读次数：本文字数： 3.1k 阅读时长 ≈ 10 分钟

前言

hashtable是实现set和map的另一种底层机制，准确来说，在C++11之后，是实现unordered_set、unordered_map、unordered_multiset和unordered_multimap这四种无序关联式容器的底层机制。

但是由于书中使用的C++编译器是C++11之前的版本，因此这里的解析在C++11标准之前，下面介绍的hashtable与正式标准存在一些差别，比如hash function的差别、C++增加了重映射策略等等。

尽管如此，这里剖析的hashtable在关键设计思想上与新标准一致，比如均使用开链法（链地址法）处理冲突，即使用bucket vector和linked list实现哈希表。

本篇主要内容有：

1.STL中使用链地址法实现hash表；

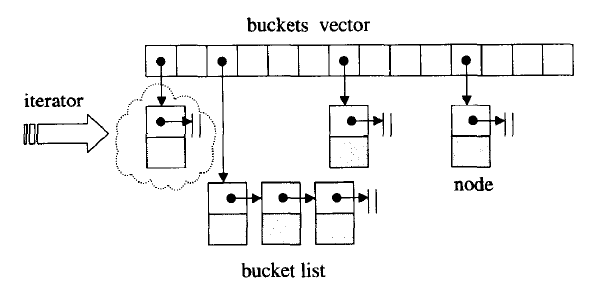
2.hashtable的迭代器为正向迭代器，递增的实现方式；

3.hashtable的构造与内存管理（插入和重整）；

4.hashtable的复制和清除操作。

hashtable

hashtable概述

hash table（哈希表）能够对于其中的元素提供常数级时间的存取和删除操作。

实现方式就是利用一个hash函数（散列函数），将元素的值value映射到一个索引范围内，比如通过取模运算将任意整数X映射到[0, TableSize - 1]，那么TableSize是哈希表的大小，索引范围就是[0, TableSize - 1]。

哈希函数的问题是：如果元素的取值空间远大于索引的取值空间，那么有可能会导致不同的元素被映射到相同的位置，也就是发生了碰撞。对于碰撞的处理有以下几种处理方式：线性探测、二次探测、开链等。

线性探测：

当通过哈希函数计算出某个元素的插入位置时，如果当前位置已经存在元素，那么就依次向后寻找（如果遇到尾部就从头开始）。

查找时如果通过哈希函数计算出的插入位置不是当前元素，也是依次向后查找，直到遇到目标元素或者空位置。

删除时只标记删除记号，实际删除操作等待表格重新整理时再进行。

这种方法的缺点是：当哈希表中负载系数增大时，插入成本会剧烈增大。（负载系数指的是哈希表中当前元素个数）也就是说，如果当前表中元素越多，那么新元素越有可能在填充过元素的地方不断向后探测，直到找到合适的位置；而这个合适的位置又会增加未来新元素的插入成本。

二次探测：

如果插入时通过哈希函数计算出来的插入位置H已经存在元素，那么向后寻找的位置依次为：$H+1^{2},H+2^2,H+3^2,…$而不再像线性探测一样为：$H+1,H+2,H+3,…$

二次探测带来的疑问：

①线性探测每次探测的都必然是一个不同的位置，二次探测能够保证如此？二次探测能否保证如果表格之中没有X，那么我们插入X一定能够成功？
②线性探测的运算过程机器简单，二次探测则显式复杂一些。这是否会在执行效率上带来太多的负面影响
③不论线性探测还是二次探测，当负载稀疏过高时，表格能够够动态成长

对于①：假设表格大小为质数，其负载系数永远在0.5以下（也就是最多只装一半元素），那么就可以确定每插入一个新元素所需要的探测次数不多于2。（注，这是书中的结论，暂时没有理解）

对于②：至于复杂度问题，一般总是这样考虑：收获的比付出的多，才值得这么做。我们增加了探测次数，所获得的利益好歹比二次函数计算所花的时间多。线性探测需要的是一个加法（加1），一个测试（看是否回头），以及一个可能用到的减法（用以绕转回头）。二次探测需要的则是一个加法（从i-1到i）、一个乘法（计算$i^2$），另一个加法以及一个mod运算。看起来得不偿失。然而中间却又一些技巧，可以除去耗时的乘法和除法：

因此，如果我们能够以前一个H值来计算下一个H值，就不需要执行二次方所需要的乘法了。虽然还是一个乘法，但那是乘以2，可以位移位快速完成。置于mod运算，也可证明并非真有需要。

对于③：array的增长。如果想要扩充表格，首先必须要找出下一个新的且足够大（大约两倍）的质数，然后考虑表格重建的成本——不仅要拷贝元素，还需要考虑元素在新表格中的位置然后再插入。

二次探测的缺点是：两个元素经由哈希函数计算出来的位置若相同，则插入时所探测的位置页相同，形成了某种浪费。消除次集团的方法也有，例如复式散列等。

开链法（链地址法）：

将所有索引值相同的元素存储在一个链表中，hash表只存储这些链表的头指针。

因此如果插入时发生冲突，也只需要在链表上增加一个结点。

搜寻时如果发生冲突，需要在链表上进行线性搜寻，但是只要链表足够短，那么速度还是非常快。

（怎么使得链表足够短？发生冲突的次数尽量少，也就是hash表尽量大）

hashtable的桶子(buckets)与节点(nodes)

SGI STL将hash table内的每一个元素称为桶子(bucket)，这样表述意思是说：哈希表中的每个单元，有可能是一”桶“元素。

哈希表的节点定义为：

template <class Value>
struct __hashtable_node {
    __hashtable_node *next; // 指向下一个节点的指针
    Value val; // 节点的值
};

需要注意的是，bucket维护的链表，并不使用STL的list，而是自行维护节点。但是哈希表，也就是bucket的聚合体，以STL的vector完成，以便有动态扩充能力。

hashtable的迭代器

hashtable的迭代器处理维持当前指向的bucket的节点的关联，还需要维持与整个hash表的关联。
这样前进操作从当前节点出发，通过节点的next指针访问下一个节点；如果当前节点恰好是当前bucket的尾端，则需要利用与hash表的关联跳转到下一个bucket上。

由于hashtable迭代器是一个正向迭代器，所以没有后退操作。

hashtable的数据结构

下面是hashtable的定义摘要，主要可以看出以vector装载buckets。

hashtable的模板参数有：

Value：节点的实值类型
Key：节点的键值类型
HashFcn：hash function的函数类型
ExtractKey：从节点取出键值的方法（函数或仿函数）
EqualKey：判断键值相同与否的方法（函数或仿函数）
Alloc：空间配置器。缺省使用std::alloc

hash function是计算元素所在桶子索引的函数，这项任务交给bkt_num函数，由它调用hash function计算一个可以执行模运算的值。

系统预定义的hash表大小：

虽然链地址法并不要求哈希表大小必须为质数，但SGI STL仍然以质数来设计哈希表大小，并且先将28个质数（主键呈现大约2倍的关系）计算好，以备随时使用，同时提供一个函数，用来查询在这28个质数之中，“最接某数并大于某数”的质数

hashtable的构造与内存管理

hashtable的构造

在hashtable的定义式中定义了以节点为单位申请空间的配置器：

节点配置函数和节点释放函数为：

hash table没有默认构造函数，构造函数如下：需要指定bucket的个数

元素插入(insert)和表格重整(resize)

键值不允许重复的插入操作

hash table以insert_unique函数完成插入元素操作：

该函数首先调用resize函数判断是否重建表格；之后调用insert_unique_noresize函数完成插入操作。

resize：表格重建与否的标准是：加入当前元素之后的元素个数与哈希表的大小（即bucket的数量）相比，如果前者大于后者就重建表格。

将其中一个旧bucket中的元素移动到新的bucket的操作图解：（下面需要将#2中的55移动到对应的新#55中）

insert_unique_noresize：经过重建处理，下面就是在不需要重建的情况下插入新节点，注意键值是不允许重复的

键值允许重复的插入操作

insert_qeual函数允许键值重复的元素插入，同样是首先调用resize尝试重建表格，但是第二步调用的不再是insert_unique_noresize，而是insert_equal_noresize函数。

判断新元素属于哪一个bucket(bkt_num)

判断元素属于哪一个bucket应该是hash function的任务，SGI在处理时包装一层，将任务交给bkt_num完成，在由此函数调用hash function，最终获得一个可以进行模运算的值。这是因为某些元素类型无法直接用于对hash table的大小模运算。

复制(copy_from)和清除(clear)操作

整个hash table由vector和linked-list组合而成，因此复制和清除时需要注意内存释放问题。

清除全部元素操作：

复制另一个hash表的操作：

hash function

hash function用于将一个元素的键值key映射到[0, N - 1]，N是hash表中的bucket个数。

SGI将这个任务交由bkt_num来完成，这是因为元素的键值类型可能是非数值，比如const char*，bkt_num调用hash function，对于不同的键值类型取得一个可以对N进行模运算的值。大部分的hash function对于char、int、long等整数类型什么都不做，只是返回原值。但是对于字符串类型，设计一个转换函数为：

由此，可以得知，如果hash funciton没有办法处理的类型，就需要用户自行定义针对这些类型的hash funciton。

笔者注：

侯捷先生使用这版SGI标准位于C++11之前，目前（2023年）的C++标准已经对于hash table进行了修订，目前的hash table采用的策略是h2(h1(k), N)，其中k表示键值，N为hash表大小，h1是一个hash function，将映射到[0, numeric_limits:::max()]，h2是一个range-hashing function，将h1(k)映射到[0, N)。另外还增加了重映射策略等等。

因此这里的hash function仅供参考，说明一种设计思想。